地面甚高频（VHF）无线电信号覆盖——超视距传播

当我们提及超视距（BLOS）甚高频无线电通信时，也包括非视距（NLOS）电路。严格来说，若非自然或人为的障碍物阻挡，非视距电路原本可能是常规的视距路径。根据地球的球面几何形状，这些非视距路径处于两个站点之间的无线电地平线范围内。另一方面，超视距通信电路本质上是超越地平线或跨地平线的电路。非视距和超视距电路的根本区别在于，在超视距的情况下，路径上是否存在山丘、山脉、建筑物等形式的障碍物并不重要，然而，路径总是会被地球球面轮廓的地形凸起所阻挡。

在本文中，为了清晰起见，我通常会将非视距电路称为受阻视距（受阻LOS）。如果需要进一步区分，我会在描述路径时说明所考虑的障碍物是地形凸起还是离散的物体。其次，正如我们在系列文章的第一部分所做的那样，从业余无线电爱好者的角度出发，我将继续使用“甚高频”一词来指代甚高频和特高频频段。

衍射的物理现象——救星

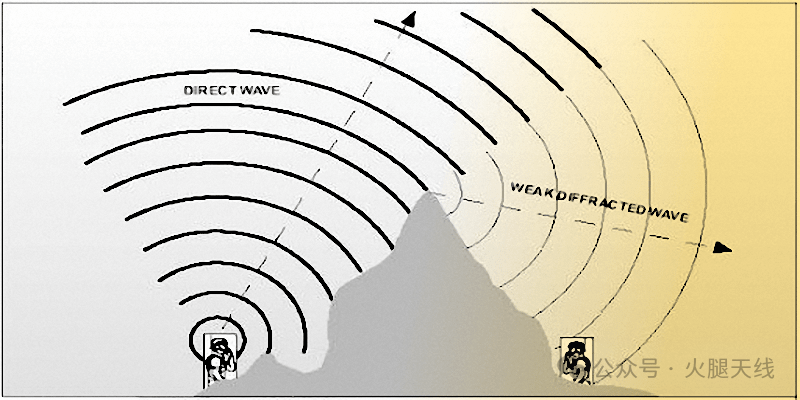
此图以图形方式描绘了无线电信号在障碍物边缘衍射的基本概念。衍射使部分无线电信号能量能够转移到障碍物后面的阴影区域。

在甚高频、特高频以及更高的微波频率下，传播的一般性质主要是直达波传播。电离层反射或表面波等现象在这些较高频率下不会发生。当然，有时可能会有一些直达波传播调制因素，比如对流层空气密度梯度导致的超折射等，这些因素可能会扩大有效无线电地平线，从而增加直达波的覆盖范围。尽管如此，还有一种至关重要的现象——衍射，它在甚高频无线电信号覆盖中起着非常重要的作用。我称它为甚高频/特高频无线电的救星…… 让我们看看为什么衍射如此重要？

当我们研究甚高频或更高频率时，它们的大多数特性开始与光波相似。就像明亮的光源被阻挡时会形成阴影一样，甚高频无线电信号也是如此。如果源自甚高频/特高频无线电发射机的传播信号遇到任何大型物体，如建筑物、山丘等，它会在阻挡物体的另一侧产生无线电阴影。无线电信号会被障碍物阻挡，从而在其后面产生“无线电盲区”（信号缺失）。位于这种障碍物阴影区域内的接收站将无法进行通信。

有没有办法让甚高频无线电信号绕过障碍物并传播到其后面呢？值得庆幸的是，有！…… 有几种解决方法。一种方法是少量无线电信号可以通过其他物体的多路径侧向反射到达障碍物后面。当然，这种方法并非普遍可行，也可能不可靠。

然而，衍射这一物理现象帮了我们的忙。尽管到达障碍物后面阴影区域、角落和缝隙的衍射信号强度可能不太强，但在特定的地形场景下，它们总是稳定存在的。衍射使我们在拐角处和阴影区域也能实现可靠通信。

跨地平线超视距传播或像非视距情况那样受阻路径的视距传播，主要也是由于衍射才得以实现。

本质上，地面甚高频无线电信号传播主要有两个不同的方面。它们是视距（LOS）模式和超视距（BLOS）模式，后者包括非视距或受阻路径的视距模式。它们都有各自独特的特点和属性。在系列文章的第一部分详细研究了甚高频无线电信号传播的清晰路径视距模式后，我们现在将研究包括非视距和超视距在内的受阻路径模式，以及它们在甚高频远距离通信（DX通信）中的综合影响。

受阻视距（LOS）或非视距（NLOS）甚高频无线电信号传播

在这个系列文章的上一篇中，我们讨论了典型的清晰路径视距甚高频无线电信号通信。这种视距无线电通信的距离限制在最大的地平线到地平线之间。在这种情况下，可能会违反第一菲涅尔区的净空要求。然而，在较短距离内，若第一菲涅尔区的净空得以保持，也可能不会产生额外损耗。实际上，如果第一菲涅尔区完全净空，理论上可能会产生高达6dB的地面反射增益，但在实际中会更低。无论如何，视距电路要么中间是畅通无阻的，要么路径上存在一个或多个自然或人为的地形障碍物。

两个天线位置之间的第一菲涅尔区受阻会导致额外的衰减。这种额外损耗的大小取决于阻挡物体侵入菲涅尔区的程度。侵入深度越大，额外损耗就越大。

虽然在第一菲涅尔区周围有无数个同心的菲涅尔区，但我们通常关注的是第一菲涅尔区。只有第一菲涅尔区会对整体传播损耗产生显著影响。菲涅尔区是发射天线和接收天线之间的一个长椭圆形区域，是两个天线之间的一个虚构且无形的区域。任何位于这个区域内的物理物体或东西，都可能根据其侵入的性质和深度，在不同程度上对传播产生不利影响。

在我们的讨论中，我们将菲涅尔区侵入区域分为两部分，分别代表不同的侵入性质。它们是反射区域和衍射区域。每当一个阻挡物体从任何一侧侵入三维椭圆形的菲涅尔区时，它就会开始影响通信电路接收端的信号强度。

如果侵入菲涅尔区的程度小于侵入处的菲涅尔区半径，那么阻挡物体不会切断从一个天线到另一个天线的直线视距直接路径。在这种情况下，菲涅尔区侵入被视为处于反射区域。在这种情况下，到达接收天线的地面甚高频无线电信号由两个分量组成。它们是视距直接路径信号和从阻挡物体顶部边缘（或表面）反射的第二个信号。视距直接路径和反射路径的长度显然不同，因此，它们会使到达接收点的信号之间产生相位差。所以，沿着这两条路径到达接收天线的信号会进行矢量相加，从而改变接收端的总信号强度。

上述现象导致的有效信号强度损失归因于反射型的菲涅尔区阻挡。

现在，如果阻挡物体的大小使其深入菲涅尔区内部，中断了视距直接路径，那么情况就会发生很大变化。虽然这仍然是菲涅尔区受阻的情况，但我们不再有视距直接路径，也没有在障碍物顶部的反射点。

此时，阻挡物体从反射物体变成了衍射物体。在这种情况下，菲涅尔区侵入被视为处于衍射区域。在这种情况下，信号既不能通过视距直接路径到达接收站，也不能通过物体反射到达。信号到达接收站的唯一途径是借助阻挡物体顶部的衍射现象。

由于在上述第一菲涅尔区内的两个区域中，起作用的传播模式截然不同，为了更好地直观理解，我们将在叙述过程中分别讨论这些子区域。现在，让我们逐一研究菲涅尔区反射区域和菲涅尔区衍射区域……

我们假设，像山丘、建筑物等阻挡物的顶部表面宽度，与发射和接收无线电台之间可能达数公里甚至更远的距离相比，几乎总是小得多。因此，在处理衍射情况时，我们将阻挡物视为典型的刃形物体。

菲涅尔区反射区域

在典型的菲涅尔区反射区域受阻场景中，发射天线和接收天线之间总会有一条清晰的视距直接路径。天线的高度通常高于阻挡物的高度。至少，发射端或接收端的其中一个天线要比阻挡物高得多，以确保两者之间有一条清晰的直接路径。

现在，有人可能会问，这有什么大不了的？一条清晰的路径难道不足以避免额外损耗吗？…… 嗯！不幸的是，事情通常没那么简单。

两个天线之间路径周围的椭圆形桶状菲涅尔区，经常会被建筑物、山丘或其他物体阻挡。即便没有这些，大多数情况下，地球的凸起也会挡在中间。即使直接路径没有受阻，任何一个或所有这些障碍物都可能部分切入菲涅尔区。就是这样…… 这种菲涅尔区受阻现象足以导致地面甚高频信号传播路径产生额外损耗。

让我们在叙述过程中，尝试直观地探索这一现象……

当两个天线之间的视距直接路径未被中断时，菲涅尔区可能会以反射模式受阻。然而，障碍物侵入菲涅尔区会导致一定程度的衰减，衰减程度与侵入程度成正比。

如相关插图所示，人们可能会注意到，菲涅尔区内阻挡物体的顶部会反射一部分信号，从而形成一条到达目的地的替代路径。视距直接路径和反射路径都从发射端出发，在接收端汇聚。然而，它们的路径长度不同，因此，在接收端，沿着这两条路径传播的信号的相位差也不同。根据这两个信号的相对强度和相位差，它们会相加，要么增强接收端的信号强度，要么使其衰减。

存在菲涅尔区阻挡时，总信号的计算遵循一定的模式，可以通过数学方法进行相当精确的计算。在总路径上不同点存在障碍物，且它们侵入菲涅尔区包络的深度不同，由此产生的衰减量可以通过数学计算得出。

我们稍后会讨论计算部分，目前让我们继续直观地深入探讨这个概念。

从障碍物顶部发生的反射过程还受其他几个变量的影响。例如，并非所有反射表面的光滑度或反射率都相同。此外，障碍物不一定总是像建筑物或山丘这样的离散物体，也可能是地球的凸起，它会在信号路径上很长一段距离内形成连续的阻挡。

更复杂的是，无线电信号的反射行为还取决于信号的频率，更重要的是，取决于其极化方式和在反射表面的入射角。水平极化信号从表面反射时，总是会发生180°的相位反转，而垂直极化信号只有在入射角约为10°或更小时，才会发生180°的相位反转。在较大的入射角下，不会发生相位反转。

现在，让我们把注意力回到菲涅尔区。有趣的是，菲涅尔区的边界区域（菲涅尔区包络）标志着会产生相同额外衰减的点。在菲涅尔区包络内，可以绘制其他对称且平行的曲线。这些封闭曲线中的每一条都代表着衰减量相等的点。

菲涅尔区外层边界内的每个同心区域都用净空比（或百分比）来表示。例如，侵入菲涅尔区20%相当于净空80%，侵入40%相当于净空60%，以此类推。无论沿着路径的侵入点在哪里，由于菲涅尔区阻挡侵入导致的衰减量在任何净空百分比值下都是相同的。

现在，让我们大致了解一下在不同程度的障碍物侵入菲涅尔区的情况下，情况会如何发展。我再次提醒，在本文中我们提到菲涅尔区时，通常指的是第一菲涅尔区。

以下是一些重要且看似奇特的事实…… 在净空61%（即侵入39%）时，菲涅尔区额外产生的损耗为0dB…… 哇！零损耗难道不应该出现在菲涅尔区边界之外吗？当阻挡物体侵入菲涅尔区边界近40%时，怎么会没有损耗呢？

嗯，我们上面说的是正确的，没有错误…… 有趣的是，当障碍物位于第一菲涅尔区的边界时，它会增强甚高频无线电通信电路接收端的信号强度。位于菲涅尔区边界的物体反射的信号，其与视距直接路径的路径长度差为信号波长的1/2。这意味着直接信号和反射信号有180°的相位差，然而，在障碍物的反射点，信号会再发生180°的相位偏移。在几乎所有实际情况下，无论信号极化方式如何，信号在反射表面的入射角都非常小，很可能总是小于10°，因此总会发生180°的反射相位偏移。我们在之前的讨论中发现了这一点，不是吗？因此，在这种情况下，沿着两条路径到达接收天线的信号会相长叠加，从而增强信号强度。理论上，这种增强约为 +6dB。

换句话说，虽然我们最初可能认为菲涅尔区边界是衰减开始的地方，但事实证明，它实际上是信号增强的地方。在一般的无线电通信术语中，这通常被称为地面增益。通常情况下，如果天线高度合理，下方的地球表面往往会产生额外的地面增益。

因此，如果障碍物位于100%净空点（0%侵入）的边界处，我们会得到 +6dB的增益。随着障碍物开始侵入菲涅尔区，+6dB的增益开始减小，直到在净空61%时变为0dB。这就是为什么即使障碍物侵入菲涅尔区近40%，损耗仍然为零。

如果障碍物更高，侵入菲涅尔区更深，衰减就会开始增加，直到当障碍物的尖端与视距直接路径相切但不阻挡它时，理论上衰减达到 -6.9dB。上述6.9dB的损耗仅适用于顶部表面较窄的阻挡物体。然而，如果是顶部较宽的表面，与视距路径相切处的损耗会更高，可能高达10 - 15dB甚至更多。

菲涅尔区衍射区域

到目前为止，我们研究了障碍物侵入菲涅尔区一半深度时的情况。如果阻挡物体足够高，切断了视距直接路径并深入该区域内部，会怎么样呢？

当然，我们会面临不同的物理情况。我们将不再有视距直接路径，它将被完全切断。我们也不会有传统的反射表面来产生替代信号路径…… 就这样完了吗？…… 这是否意味着我们再也无法通信了？…… 哦，不，在这种情况下还有其他物理现象起作用。现在，衍射现象占据了主导地位。

当菲涅尔区侵入深度超过菲涅尔区半径，中断了视距路径时，就被视为进入了衍射区域侵入。在这种情况下，衰减可能会相当大。


在地面甚高频无线电信号传播到障碍物后面的阴影区域的情况下，掠过障碍物边缘的信号会产生一些小波，这些小波会照亮障碍物阴影中的区域。阴影区域中的信号强度取决于几个因素，包括信号的波长（频率）、障碍物的大小和形状、发生衍射的边缘的尖锐程度等等……

此外，衍射路径的几何形状和衍射角度也起着重要作用。参考插图中障碍物尖端标记为θ的角度。角度θ越大，阴影区域中的衍射信号就越弱。

由于衍射损耗随着角度θ的增大而增加，合理的假设是，当侵入物体对菲涅尔区视距线的阻挡只是轻微的，那么角度θ会很小，损耗也会很小。因此，随着侵入深度进一步增加，角度θ也会变大。结果，菲涅尔区阻挡衍射损耗也会更大，接收天线处的信号会变弱。

因此，发射端和接收端之间的障碍物越高，衰减就越大。高山往往会在其后方产生无法进行通信的阴影区域，而较小的山丘虽然会使信号大幅衰减，但信号可能仍然足够强以维持通信。同样，在山的阴影一侧靠近山脚的区域可能接收不到足够强的可读信号，但当远离山脚，减小角度θ后，经过一定距离，信号接收可能又会突然变得可行。

让我们更深入地研究整个过程。我们将看到菲涅尔区原理的应用如何解释我们上面讨论的所有内容，并将所有内容整齐地整合为一个逻辑整体。它不仅能解释由于衍射导致的阻挡损耗，还能解释我们在上一小节中讨论的反射型衰减。

接下来的论述对我们中的一些人来说可能数学性更强一些。不过，我建议大家试着理解一下，这将有助于解释甚高频无线电信号在各种障碍物以及地球地形曲率上的远距离传播机制。在接下来的部分，我们将介绍计算菲涅尔区阻挡损耗的方法。

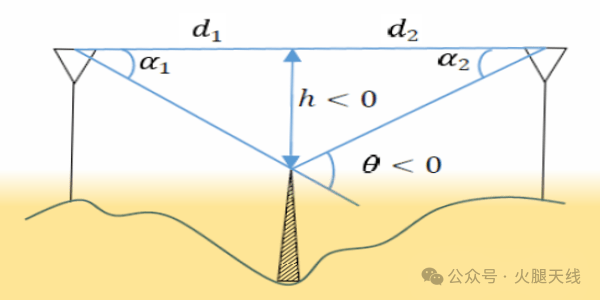
在与当前讨论部分以及之前关于菲涅尔区反射区域相关的插图中，我们标记了一些距离和角度变量。我们不会深入探讨推导以两位伟大科学家命名的菲涅尔 - 基尔霍夫衍射参数（υ）所需的大量数学过程，而是直接给出公式，并应用它来计算在反射区域或衍射区域阻挡的各种情况下，菲涅尔区阻挡损耗的大小。目前，简单的几何计算就足以满足我们的目的。

菲涅尔 - 基尔霍夫衍射参数的几何定义如下：

υ = h x √((2/λ) x (d1 + d2)/(d1 x d2))

其中：

- υ是计算得到的菲涅尔 - 基尔霍夫衍射参数。

- h是障碍物相对于中心视距路径的高度。

- λ是无线电信号的波长。

- d1和d2分别是发射端和接收端到障碍物的距离。

注意：请记住，υ是一个无量纲参数。其他变量，如高度、波长和距离，必须使用相同的度量单位。不能混用米和千米，或者英尺和英里等单位。如果波长的单位是米，那么障碍物的高度以及发射端和接收端到障碍物的距离也都必须是米。障碍物的高度（h）是相对于中心视距路径线来测量的。如果障碍物的顶部在视距线下方，比如在反射型障碍物的情况下，参数h为负值。另一方面，如果障碍物穿过视距线，比如在衍射型障碍物的情况下，“h”的值为正值。

在正常情况下，上述计算菲涅尔 - 基尔霍夫衍射参数的公式普遍适用。然而，在特殊情况下，比如城市杂波环境中甚高频无线电信号通过附近高楼的屋顶衍射在城市天际线上传播时，上述公式可以通过合理的近似进一步简化。

在典型的建筑物屋顶衍射导致的城市杂波传播场景中，d1和d2这两个距离会变得极不对称，因此可以进行如下近似。到附近建筑物衍射点的距离d1短得多，通常在几十米的范围内，而到接收端远端的距离d2，也就是跨越天际线的距离，可能有几千米（几千 米）。这意味着d1 << d2。

如果我们在上述公式的分子中忽略d_{1}对d1 + d2的影响进行近似，公式可以简化为：

υ = h x √(2/(λ x d1))

不过，请记住，上述简化仅适用于上述场景或任何d1 << d2的类似情况。

现在我们已经推导出了菲涅尔 - 基尔霍夫衍射参数，接下来就很简单了。只要衍射点可以归类为刃形衍射，我们就可以使用一个相当精确的近似公式来计算该点的信号衰减损耗。在大多数情况下，这应该不成问题，因为典型的人造障碍物，如建筑物，以及自然地形物体通常都可视为窄顶障碍物。然而，也有一些例外情况，衍射表面可能是宽顶、光滑或弯曲的。这将与单点刃形衍射场景有很大差异。地球的凸起就是这样一个例子……

我们将在下一节讨论这个问题，现在让我们先了解如何计算在地面甚高频无线电信号传播场景中经常遇到的典型单点刃形衍射损耗。下面我给出计算衍射损耗（以分贝（dB）为单位）的公式。只要计算出的菲涅尔 - 基尔霍夫衍射参数υ ≥ -0.7，这个公式的结果就相当准确。在大多数实际情况下，这应该是没问题的。

L(dB) = 6.9 + 20 x log(√((υ – 0.1)2 + 1) + υ – 0.1)

在许多情况下，当菲涅尔 - 基尔霍夫衍射参数υ的数值远大于0.1时，上述公式可以进一步简化，且不会引入显著误差，简化后的公式如下：

L(dB) = 6.9 + 20 x log(√(υ2 + 1) + υ)

如果在甚高频无线电信号传播电路中，由于不同位置存在多个障碍物而有多个衍射节点，那么必须分别计算每个节点的衍射损耗，然后将它们累加起来。在这种情况下，如果节点处的衍射角度较大，所有衍射节点的总损耗可能会迅速增加到难以接受的程度。

超视距（BLOS）甚高频无线电信号在地形凸起上的传播

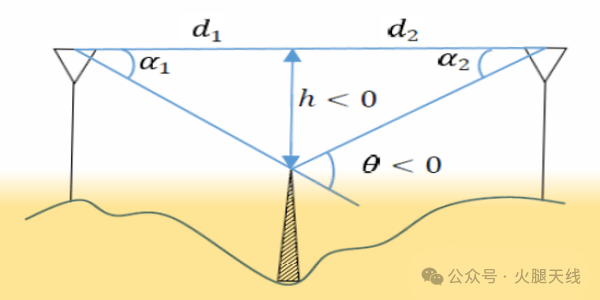
此图展示了一种简化流程，用于找到一个等效的虚拟单点刃形衍射障碍物，其产生的衍射损耗大小与两个级联障碍物场景中可能出现的情况类似。这个概念有助于简化模拟地形凸起衰减情况所需的数学方程。

在我们的论述到这里时，是时候将注意力转向那些阻挡物体不符合我们对刃形拐角障碍物定义的情况了。物体的顶部或其他可能发生衍射的部位可能并不窄，它可能是像高原那样的宽阔表面，甚至可能是像地球自然球形凸起这样的弯曲表面。在所有这些情况下，通常不再是围绕单个边缘的衍射情况。因此，为简单单点刃形衍射所做的计算不再适用。

与其试图寻找计算各种任意形状几何物体周围衍射损耗的方法，我们不如继续关注地球的地形凸起。此外，我们将避免使用那些可能更精确但对我们的目的来说过于复杂的数学模型。因此，现在我将介绍一种相当不错的近似方法，可应用于我们的地球曲面模型。我们的方法不仅适用于地形凸起的情况，对于估计桌状高原上的衍射损耗也相当有效。

请记住，当我们讨论地面甚高频无线电信号在地球地形凸起曲面上的传播时，我们仍然假设存在具有正常折射率梯度的标准大气。在本文中，我们不涉及超折射或对流层波导现象，这些现象可以使甚高频无线电信号的覆盖范围大幅扩展。即使对流层折射梯度保持正常，它也能使甚高频信号绕过障碍物和弯曲表面传播。

参考相关的等效刃形图，当处理两个或更多衍射点时，我们可以很好地进行近似。虽然这是一种近似，但对于大多数目的来说已经足够精确。如果我们确定障碍物表面上的两个拐角焦点，它们会产生与衍射点相切的路径，我们可以通过几何方法延长切线，使其相交。这个虚拟点现在代表一个具有特定高度、位置和顶角的等效单点障碍物，其表现与从障碍物表面边缘的两个衍射点产生的累积衍射效应非常相似。查看插图中这种近似的几何原理。

通过迭代上述过程，任何任意或不规则形状障碍物上的多个衍射点都可以转换为一个数学等效的单点衍射点。一旦完成转换，所有其他计算过程都可以归结为单点衍射模型。尽管在这个过程中会引入少量误差，但最终结果在大多数场景中都足够精确，具有实际可接受性。

实际上，在围绕地形凸起传播时，信号会沿途遇到多个级联的短距离衍射段，每个短衍射段都受到地形偏差的影响。每个段的距离、障碍物高度和衍射顶角都很小，因此每个段的衍射损耗贡献也很小。然而，它们会逐级累积，在弯曲的地形上形成很大的总衍射损耗。我们的单点近似模型得到的衍射损耗几乎等于上述各段损耗的总和。

我不会详细讲解推导我们所讨论的等效虚拟单点刃形障碍物公式所需的基础几何知识，感兴趣的读者可以自行尝试推导。

现在，让我们继续探索一个更现实的实际甚高频无线电信号衍射场景。在研究地球曲面地形凸起模型之前，让我们先定义一些参数，并熟悉一些有用的数学公式。

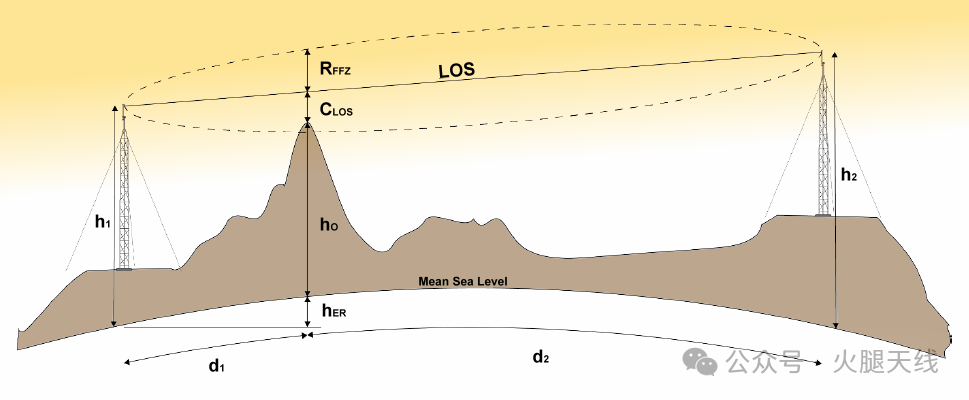
此图展示了一个简化但现实的菲涅尔区净空路径剖面图，标记了所有所需的变量。这个剖面图将用于给出一组数学公式，用于计算各种类型的甚高频传播损耗。

看一下上面的插图。它展示了一个典型的点对点短距离视距传播路径，其中有一个障碍物部分侵入了路径的第一菲涅尔区。在这个示例场景中，天线高度彼此不同，障碍物的位置是任意且不对称的。这样做是为了涵盖所有常见的变量。此外，该场景还考虑了地球的曲率，以及由于地球曲率导致的障碍物高于地面可见高度的额外高度。

与我们的讨论相关的所有变量以及后续的数学公式都标记在上面的插图中，因此应该不会有歧义。

话不多说，开始吧……

在我们的论述中，除非另有明确说明，在接下来的每个数学公式中，所有距离，如d、d1、d2、dOP等，必须以千米为单位，而所有波长(λ）或高度，如h、h1、h2、hO、hER、RFFZ、CLOS等，必须以米为单位。这一点很重要，因为为避免混淆，我已经将地球半径等几个常数进行了归一化处理，以便与上述单位配合使用。

现在，这是我们要介绍的第一个相关参数，即菲涅尔区半径（RFFZ）。由于菲涅尔区是桶形的，其长度方向上不同点的半径会有所不同。最大半径位于视距路径的中点，随着靠近天线两端，半径会逐渐减小。

RFFZ = 31.62 x √(λ x d1 x d2 / (d1 + d2)) 

接下来，让我们计算另一个参数，即由有效地球半径引起的障碍物额外高度（hER），在上面的插图中标记为hER。

hER = (d1 x d2) / (12.74 x K)

其中，K是有效地球半径因子，由对流层折射率梯度决定。在标准大气的典型条件下，K = 1.33。在超折射条件下，K > 1.33，而在亚折射条件下，K < 1.33…… 对于典型的甚高频无线电信号传播场景，我们使用K = 1.33。不过，我给出的这组公式能够考虑任何折射率梯度，因此支持任何K值。

下一步是计算相对于直接视距路径的菲涅尔区障碍物净空距离，在我们的插图中表示为CLOS。要计算这个值，需要将障碍物高于地形的高度（hO）与hER相加，得到障碍物的有效总高度。然后，从天线之间倾斜的直接视距路径在障碍物位置处的高度中减去这个有效总高度…… 是不是有点复杂？别担心！下面是用于计算菲涅尔区净空CLOS的合并简化公式。

CLOS = h1 + ((h2 - h1) x d1 / d) - hER - hO

在本文前面讨论各种受阻视距（NLOS）路径时，我们定义了相对于两个天线之间直接视距路径（也是菲涅尔区的中心轴）的菲涅尔区障碍物高度（h）。任何穿过视距路径切断直接路径的障碍物，h > 0，而反射型菲涅尔区侵入的情况下，h < 0 。

现在让我们看看在我们的例子中，菲涅尔区障碍物高度是多少。通过合并和重新整理上述两个公式，可以得到：

h = hO + hER - h1 - ((h2 - h1) x d1 / d)

请注意，插图中所示的障碍物高度hO直接适用于像山丘、山脉或建筑物这样的离散障碍物。然而，对于像地球地形这样的大曲率情况，hO将是平均地形海拔高度（AMSL）与该地形上任何实际或虚拟物体额外高度的总和。

就是这些…… 这些就是我们目前需要推导的变量…… 现在，下一步是应用我们之前给出的两个公式来计算菲涅尔 - 基尔霍夫衍射参数（υ），然后计算以分贝为单位的衍射损耗。

回顾一下，再次给出这些公式。请注意，我在下面的公式中引入了一个乘数常数0.0316，这是为了将距离单位归一化为千米，同时保持高度单位为米……

υ = 0.0316 x h x √((2/λ) x (d1 + d2)/(d1 x d2))

以及……

LDIFF(dB) = 6.9 + 20 x log(√((υ - 0.1)2 + 1) + υ - 0.1)

如果按照上述计算步骤进行，在假设为刃形衍射的情况下，我们将能够顺利计算出典型的单障碍物地面甚高频无线电信号传播电路中总的菲涅尔区衍射损耗大小。

到目前为止，一切顺利……

好啦！…… 那么，我们完成了吗？…… 还没有！我们已经很接近了，但要计算出地形凸起上超视距（BLOS）传播的总损耗，还需要再做几步。让我们马上解决这个问题……

查看下面的插图。它描绘了地面甚高频远距离通信（DX）电路在地形凸起上的所有主要关注点，可用于进一步分析。在这条地面路径的两端，我们有天线（Ant - 1和Ant - 2），它们的高度分别为h1和h2。由于这条DX电路上存在地形凸起，直接视距通信是不可能的。两个站点之间的直接视距路径（黄色虚线）深埋在地球表面以下。从白色的菲涅尔区边界曲线可以看出，菲涅尔区也严重受损。因此，在这个假设情况下，损耗会非常高，可能难以克服。不过，请记住，此插图中所示的地形凸起是为了突出概念而高度夸张的。在正常情况下，由于地球的巨大尺寸，曲率的影响要小得多。

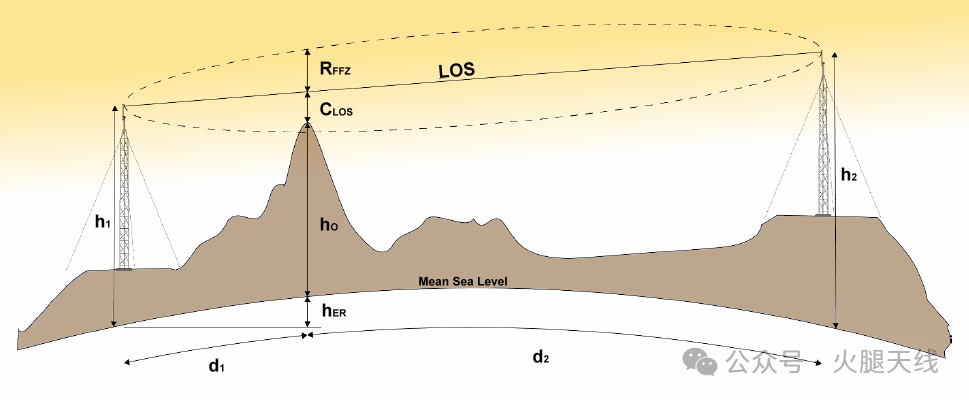
此图展示了超视距甚高频远距离传播路径中典型场景的夸张且不成比例的视图。各站点超出了无线电地平线限制，因此电路的一部分必须通过其他方式传播，比如在地球曲面上进行衍射。

无线电信号传播有两个明确的路径段，它们是两个天线位置各自的无线电地平线距离。这些无线电地平线点在插图中已标记。从每一侧到其相应的无线电地平线都有清晰的传播路径。整个甚高频无线电信号传播电路中，剩下的中间部分被地球的凸起阻挡。这个凸起部分将是电路的衍射路径段。

大家可能还注意到，在插图中，从每一端超出无线电地平线的射线用虚线延长，在天空高处相交于一点。这个交点就是我们之前解释过的单点虚拟刃形衍射点。

为了计算我们传播路径上延伸的地形凸起段的衍射损耗，我们将使用这个虚拟单点衍射点。为此，我们已经准备好应用一组数学公式。

然而，我们首先需要解决一个小问题。到目前为止，我们还不知道虚拟等效单点衍射物体的高度。在插图中，这个高度由一条黄色线表示，从虚拟衍射点顶点向下延伸，一直到埋在地球内部的视距路径。我们需要求出这条代表障碍物高度的黄色线的长度。

虚拟障碍物高度（黄色线）分为两部分，一部分在地球表面以下，另一部分在表面以上。我们有办法求出这两部分的长度，然后将它们相加得到虚拟障碍物的总高度…… 我们该怎么做呢？…… 一点也不难，继续往下看……

地球表面以下部分的虚拟高度可以通过我们已有的公式求出hER参数得到。

我将略过推导过程，直接给出适用的公式。在我们的情况下，这个高度将等同于我们为表面以上障碍物高度指定的hO参数……

hO = (dOP / (7.14 x K))2 + Average Terrain Height (AMSL)

其中……

dOP是由于地形凸起导致的受阻路径的表面长度。

这个受阻路径距离（dOP）等于总路径长度（d）减去两个天线（Ant - 1和Ant - 2，高度分别为h1和h2）各自的无线电地平线距离之和。因此……

dOP = d - (3.57 x K √h1n) - (3.57 x K √h2n)

基于上述内容，我们现在可以求出d1和d2的值，它们是从任意一个天线到障碍物位置的距离。

d1 = (3.57 x K √h1n) + (dOP / 2)

请注意，在上述两个公式中使用了h1n和h2n，它们是相对于平均地形海拔高度（AMSL）归一化后的高度。另一方面，常规变量h1和h2代表海拔高度（AMSL）。

d2 = d - d1

将这些值代入计算hER的公式中，我们将得到地形凸起表面以下虚拟障碍物部分的高度。

此时，我们已经准备好所有变量，可以计算菲涅尔 - 基尔霍夫衍射参数（υ）了…… 由此可以计算出地面电路上预期的衍射损耗。

最终，总衰减将等于整个距离的自由空间损耗与衍射损耗之和。当然，由于地球表面的性质、植被等因素还会有其他较小的损耗，但在甚高频远距离通信（DX）电路中，它们的总和要小得多。

地面甚高频远距离通信电路总损耗的计算——一个实际例子

在结束本文之前，让我给大家展示一组可应用于实际场景的真实计算。在我所举的例子中，甚高频无线电信号传播电路是位于印度北部平原的一条远距离通信（DX）路径。我们现在来分析穆索里（Mussoorie） - 新德里的2米甚高频链路。穆索里是位于北部喜马拉雅山脉山麓的一个山城…… 顺便说一下，对于那些感兴趣的人来说，喜马拉雅山也是珠穆朗玛峰的所在地。

从穆索里山上的多个位置，印度北部平原的广阔区域尽收眼底，这使得甚高频/特高频远距离无线电通信可以轻松覆盖到平原地区。在标准大气折射率梯度下，从穆索里的实际覆盖距离沿着半径为270 - 300千米的弧线延伸。在超折射情况下，覆盖范围还能再延伸几百千米。2米甚高频的地形覆盖区域通常跨越150°的弧线，面积至少为90,000 - 100,000平方千米。这里有一张地图展示了典型的覆盖范围。

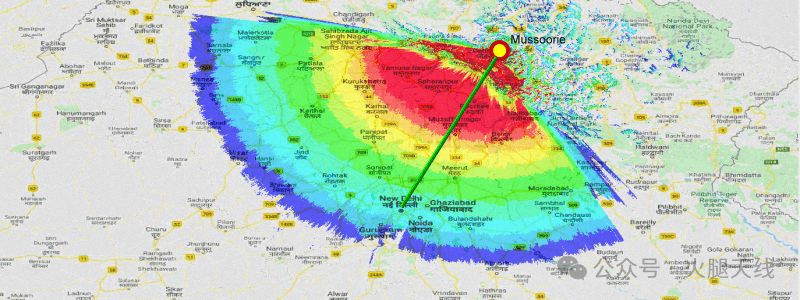
印度北部平原2米波段甚高频无线电信号传播地图示例。假设发射机（中继器）位于印度穆索里，它能向包括我在新德里的电台位置（QTH）在内的多个邦和城市提供强大的无线电信号覆盖。

在下面的例子中，我将对穆索里和我（VU2NSB）在印度新德里家中的电台之间的2米甚高频无线电信号传播电路进行链路损耗计算。查看下面插图中所示的链路路径剖面图，该图在地形剖面图上标记了通信电路的两端、路径距离和天线高度。以下是我们在示例中使用的路径变量：

- 总路径距离d = 210千米。

- 穆索里的地形高度 = 海拔1783米（AMSL）。

- 穆索里的天线高度h₁ = 1783 + 3 = 1786米（AMSL）。

- 新德里的地形高度 = 海拔218米（AMSL）。

- 新德里的天线高度h₂ = 218 + 28 = 246米（AMSL）。

- 北部平原的平均地形高度 = 海拔218米（AMSL）。

- 地球半径 = 6371千米。

- 有效地球半径因子K = 1.33（4/3）。

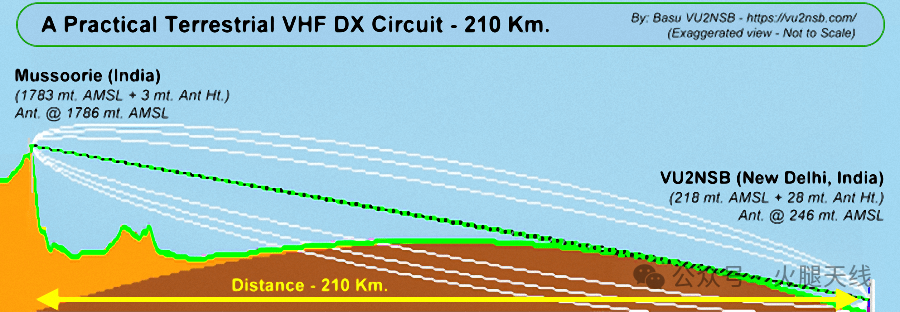
从印度穆索里山区到北部平原新德里的实际2米甚高频无线电信号传播电路。下面将计算该电路的路径损耗，包括地形凸起的衍射损耗。此例中使用的计算方法可用于计算任何地面甚高频或特高频无线电通信电路的路径损耗。

根据上述插图和列表中的路径数据，我们开始计算。所有计算均基于我们上面给出的公式。在这个阶段，我们将按逻辑顺序应用相关公式以得出我们想要的最终结果。因此，在下面的计算过程中我不会提供过多解释性叙述。

计算无线电地平线距离时，需要将天线高度相对于平均地形高度进行归一化处理。

- 对于地形归一化天线高度为1786 - 218 = 1568米的天线1，其无线电地平线距离为：

无线电地平线距离（天线1） = 1.33×3.57×√1568 = 163千米。

- 对于地形归一化天线高度为246 - 218 = 28米的天线2，其无线电地平线距离为：

无线电地平线距离（天线2） = 1.33×3.57×√28 = 22千米。

接下来……

- dOP = 210 - 163 - 22 = 25千米。

- d1 = 163 + 25÷2 = 176千米。

- d2 = 22 + 25÷2 = 34千米。

- hO = (25÷(7.14×1.33))² + 218 = 225米。

- hER = (176×34)÷(12.74×1.33) = 353米。

- h = 225 + 353 - 1786 - ((246 - 1786)×176÷210) = 83米。

- υ = 0.0316×83×√(2÷2×(176 + 34)÷(176×34)) = 0.49。

- 最后……

LDIFF(dB) = 6.9 + 20×log(√((0.49 - 0.1)² + 1) + 0.49 - 0.1) = 10.2分贝。

我们现在得到了示例中这条210千米长的甚高频无线电信号传播电路的衍射损耗数值，计算得出的衍射损耗约为10.2分贝。

为了求出预期的总路径损耗，我们还需要加上210千米路径的自由空间路径损耗分量。我们之前的讨论中已经知道，可以应用弗里斯传输方程（Friss Transmission Equation）来计算，如下：

Lfree - space = 20×Log(d) + 20×Log(f) + 32.4 = 122分贝。

如果我们把自由空间损耗、衍射损耗以及另外5 - 8分贝的杂项损耗相加，那么我们示例中的甚高频无线电链路总衰减将为……

LossTOT = 10.2 + 122 + 8 = 140.2 ≈ 140分贝。

这是一个实际的传播电路示例。在路径衰减为140分贝的情况下，仍存在良好的通信前景和强信号。一个标称功率为5 - 10瓦的2米发射机就能产生不错的信号。两端配备25瓦基站和增益为1 - 3dBi的中等天线，在调频（FM）模式下可以轻松产生可靠的S9信号且完全无噪声。

然而，请不要认为甚高频无线电信号总是能实现这么长距离的传播…… 并非如此。在这个例子中，穆索里山城的天线有效高度为1568米，且下方地形视野开阔。

使用上述讨论的方法，可以较为准确地计算实际地面甚高频无线电通信电路的衰减。